Binary Search Tree

A Binary Search Tree (BST) is a node-based binary tree data structure which has the following properties:

The left subtree of a node contains only nodes with keys lesser than the node’s key.
The right subtree of a node contains only nodes with keys greater than the node’s key.
The left and right subtree each must also be a binary search tree.
There must be no duplicate nodes (But can handle duplicates using count).
O(n) worst case can be encountered when a tree is created by adding data already in sorted order

BST

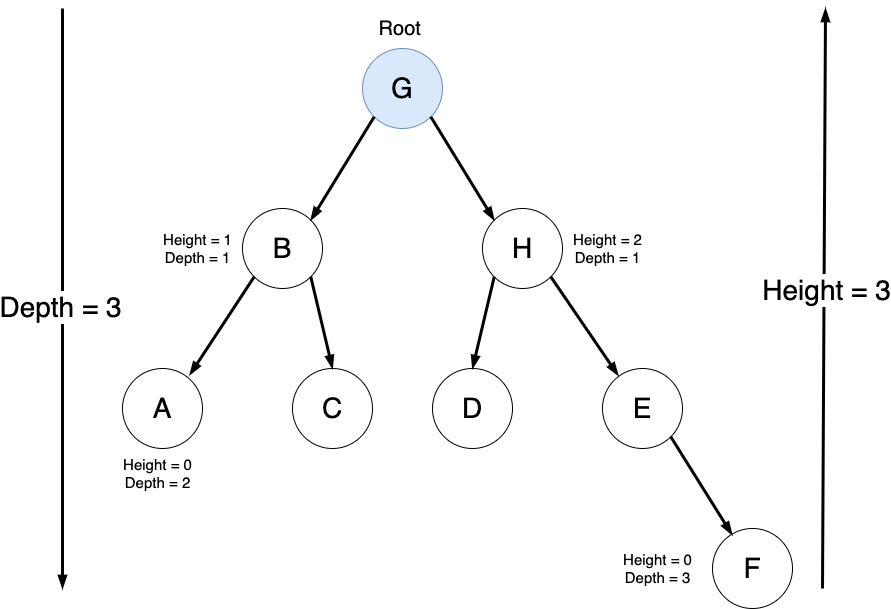
Characteristics of a Binary Search Tree

Ordered Structure: BST is an ordered or sorted data structure, which allows for efficient search, insertion, and deletion operations.
Dynamic Size: The size of the BST can dynamically increase or decrease, depending on the number of elements.

Advantages

Efficient Searching: BST enables average time complexity of O(log n) for search operations.
Ordered Data: BST keeps the elements in a sorted order, which is beneficial for range searches and ordered data retrieval.

Disadvantages

Skewed Tree: In the worst case, especially when not balanced, BST can become skewed, resembling a linked list with time complexity degrading to O(n).
Complexity in Balancing: Maintaining a balanced BST (like AVL or Red-Black Tree) requires additional logic and rotations.

Basic Operations (if balanced)

Insertion: Add a new node while maintaining the BST properties. O(log(n))
Deletion: Remove a node and rearrange the tree to preserve BST properties. O(log(n))
Search: Find a node with a given value. O(log(n))
Traversal: Visit all nodes in a specific order (e.g., in-order, pre-order, post-order).

BST_Node.h

template <typename T>
class BSTNode {
public:
    T key;
    BSTNode *left, *right;

    BSTNode(T value) : key(value), left(nullptr), right(nullptr) {}
};

BST.h

template <typename T>
class BST {
public:
    BST() : root(nullptr) {}

    // Methods for insertion, deletion, search, and traversal
private:
    BSTNode<T> *root;
};

PREVIOUSStack